日月交食 (1) ：交點月

$11$月$30$日(星期一)可見天文現象半影月食，臺灣也可以看到，傍晚月出時即帶食，歷時約$2$小時$53$分左右。在半影月食時，因為地球並非完全擋住太陽的光線，只會稍微降低月球亮度，通常用攝影的方式較容易看出變化。 之所以會有半影月食，與月球繞地軌道與地球、月球大小比例有關，下圖是示意圖，並非按照正確比例繪製：

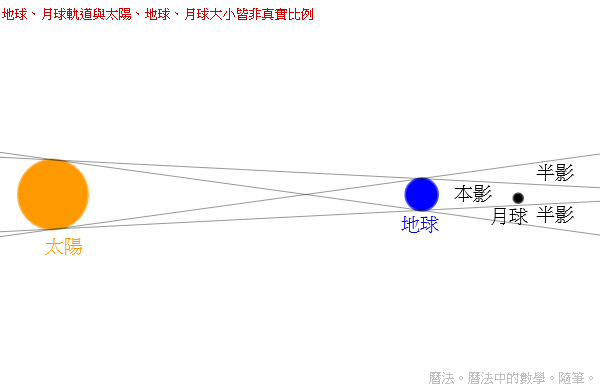
可以看到在半影區內，太陽的光線仍有部分可直射至月球，僅有在本影區內，太陽直射月球的光線才會完全被地球擋住。 若是按照地球、月球大小與軌道真正的比例繪製，可見下圖，此圖的月球繞地軌道、白道黃道交角皆按真實比例繪製：

上半部是以直視黃道面的方式來觀看月球繞地運動，此時的太陽固定在左方，但因為距離太遠無法在此圖中出現。本影、半影區的繪製也與第一張圖的繪製方式相同。下半部則是從地球上觀察本影半影區，影片中也可看到月球在運動至最右側時 (即「望」的相位) 掃過半影區。此圖的月球運行非常類似$11$月$30$日該次的半影月食(不過此圖僅為該次半影月食示意圖，不是百分之百模擬)。圖中本影、半影區的大小其實有很細微的變化，是因為地球繞日、月球繞地軌道非正圓，因此地球距太陽、月球距地球的距離皆會有細微變化，造成本影、半影區的大小非固定。

---

預測日月食是古代東亞曆法中非常重要的一環，也是少數預測的天象可以用最簡單的方法驗證的，不同如節氣或是朔望，日月食是非常視覺性、一翻兩瞪眼的天象，在古代曆法中也下了很大的工夫在此。

在介紹古代東亞曆法關於日月交食的計算前，還有許多數學與計算要先慢慢介紹，無法在單一文章中詳細解說，還請讀者們之後耐心閱讀。這篇文章要先簡單介紹關於日月交食中，最基本的概念：交點月。

關於月球運動有許多週期我們已經介紹過，如【朔日定初一：從除夕是哪一天談起】與【古代怎麼推算朔日 (1)：概論】等皆有提及的「朔望月」，或是【月球運動 (1)：平朔、定朔概論】中雖沒提到但是其實有應用到的「近點月」，也就是月球運動從近地點算起環繞回近地點所需的時間。

而因為月球繞地軌道並非與黃道面平行，有一個約$5.3$度的交角，因此每隔一段時間便會運行至黃道面，若以地球北極為上方，則月球會不斷地「上升至黃道」或「下降至黃道」。「上升至黃道」的那個交點稱為「升交點」，「下降至黃道」的交點稱為「降交點」。月球回到同一個「交點」的週期便稱為「交點月」，平均約$27.212220$天。雖然日後計算日月食不一定直接利用此一數據，但能準確觀察記錄對於日月食的預測有極大的幫助，如果「升交點」或「降交點」剛好位於「朔」或「望」的相位，便會有日月食的情況出現。

下圖是模擬月球繞地運行，太陽固定於同一點，此圖中是在圖中左側的位置，因為比例的關係太遙遠了無法畫出。圖中是以直視黃道面的方式呈現，若運行到最左側是「朔」的相位，若是最右側則是「望」的相位。上半月時，圖中的月球會由左至右運行，下半月時則是由右至左運行：

圖中可見月球繞地軌道並非於黃道面重合，而有一交角。因為月球繞地時同時也在繞著太陽運行，所以月球繞地的交角的方向也隨之改變，但若是單純只因此方式改變方向，讀者們可能會期待每隔$365.2422$天，月球繞地的角度會回到原來的方式，但事實上此「交點月」如同絕大多數的週期都有「進動」的現象，每隔$18.6$年左右「升交點」與「降交點」才會回到地球、月球相對位置中相同的位置。

此圖是按照真實軌道與進動方式模擬，甚至也考慮了地球繞日的橢圓軌道，因此圖中的「朔望月」與「交點月」的長度皆符合真實世界的長度。讀者們可以仔細觀察，約每隔$29.5$天，月球會回到「朔」或「望」的相位，而每隔約$27.2$天左右，月球會從到「升交點」或「降交點」處開始形成一週期回到該「交點」處。

在古代東亞曆法中，最先計算出「交點月」的是大家熟知的祖沖之(西元 $429$ 年－$500$ 年)，在其提出且日後使用的大明曆 (西元 $510$ 年－$589$ 年)中便提出了該數字：

【宋書志第三曆下】

會周，七十一萬七千七百七十七。 通法，二萬六千三百七十七。

這裡使用的數字是 $\frac{717777}{26377} = 27.21223$ 跟上述現代測得的數據 $27.212220$ 已經非常接近了。

這篇文章僅是簡單介紹「交點月」，在未來一系列的文章我們會慢慢介紹古代曆法怎麼計算日月交食，請讀者們日後繼續閱讀了！

月球運動 (1)：平朔、定朔概論

在【太陽運動 (1)：史書中暗藏的正弦函數】一系列文章中，我們得知了在西元6世紀時東亞終於慢慢掌握到太陽的不均勻視運動。這個現象除了影響與太陽有關的推算之外，同時也影響了朔望月的計算。在這篇文章中，我們會解釋太陽的不均勻視運動如何影響朔望月的長度，同時也會介紹另一個影響朔望月長度的「月球橢圓軌道與其進動現象」。

古代東亞的曆法一直到唐代「戊寅元曆」(西元619年 - 西元665年) 前都是使用「平朔」，戊寅元曆開始嘗試使用「定朔」但因為出現連續四個大月又改回「平朔」，下一部曆書「麟德曆」(西元666年-西元728年) 改用修正版的「進朔」，而一直到了大元時的「授時曆」(西元1281年-西元1387年) 才真正採用「定朔」。關於「進朔」的使用我們會在日後說明。

所謂的「平朔」即每個「朔望月」都採用相同長度，各部曆書上使用的數字略有不同，從最早的「太初曆」使用的數字29.5308642天，之後的幾部曆書如西元237年啟用的「景初曆」使用的數字29.530599天就已經很接近現代「平均朔望月」觀測的數字29.530588天。因為月球繞地球公轉週期遠小於地球繞日週期，「朔望月」的觀測數值相較也相對容易得多，也因此「朔望月」的數字自然比「回歸年」的數字更早接近當代的數值。

但不管數字為何，平朔採用的方式是每個朔望月長度相同，以現代的數字來說就是29.530588一直累加下去，我們在【古代怎麼推算朔日 (1)：概論】也曾提到過去如何使用平朔來計算朔日。

使用「平朔」會造成的現象是大小月會交替出現，而大概在第17個月會出現連續大月。原因很簡單，因為朔望月的平均天數剛好略大於29.5天，大月小月交替是必然的結果，讓我們來實際操作看看吧。

假設第一個合朔時分是在該日凌晨0時0分，那我們知道下一個朔日即是29.530588天後，也就是過了完整的29天，第30天會是下一個月的朔日，亦即第一個月的長度是29天。繼續算下去29.530588繼續加29.530588為59.061176，也就是從最初開始過了完整的59天，第60天是新的月之朔日，換句話說第二個月的長度是30日。

如此操作下去，我們計算看看前60個月每個月的長度為多少日，請見下表：

1	29	30	29	30	29	30	29	30	29	30	29	30	29	30	29
16	30	30	29	30	29	30	29	30	29	30	29	30	29	30	29
31	30	29	30	30	29	30	29	30	29	30	29	30	29	30	29
46	30	29	30	29	30	30	29	30	29	30	29	30	29	30	29

我們可以看到確實大小月交替出現，第17個月會出現連續大月，這是使用「平朔」時的必然結果，同時也不可能出現連續小月。

後來古代東亞慢慢能掌握「朔望月」的實際長度而非平均長度後，便慢慢想改成更貼近真實狀況的「定朔」了，也就是照著實際「朔望月」的真實長度來定每個月的長度。

詳細的計算方式會在日後慢慢介紹，讓我們先來看一下影響「朔望月」長度的幾個比較重要的因素，第一個是「月球橢圓軌道與橢圓軌道的進動現象」，請見下圖。

上圖的月球軌道並非實際比例，除該軌道半長軌有放大之外不然會根本看不到，離心率也放大10倍方便讀者觀察想像，月球橢圓軌道的離心率約0.0549，視覺上其實是個很接近正圓的橢圓。圖中我們可以看到，月球軌道的長軸有在緩慢旋轉，大約以8.85年左右旋轉一圈，讀者若有耐心的話看到最後應該可以看到該軸終於轉完一圈。因為月球繞地也因橢圓軌道的關係同樣也是不均勻的視運動，若朔的相位接近「近地點」時，則該朔望月的長度會較短，相反地，朔的相位接近「遠地點」時，則該朔望月的長度會較長，加上此長軸的緩慢旋轉即「進動」的現象，造成每個「朔望月」的長度便稍微有不同。

另一個影響因素倒不直接跟月球有關，而是一直提及的太陽視運動的不均勻現象，請見下兩圖(為方便讀者觀察與想像，地球與月球的橢圓軌道都誇大繪製，實際上的軌道都很接近視覺上的正圓)：

我們可以看到在地球接近「近日點」的時候，因為地球繞日的角速度較快，月球回到「朔」要花更長的時間，圖中的天數遠超過我們認知的長度，因為這些軌道並非實際上的橢圓軌道。

上圖是離「近日點」較遠處，因為地球繞日的角速度較慢，因此月球回到「朔」的天數便短得多，我們可以看到相同的天數月球已經繞過「朔」，而進到下一個月了。

上兩圖同時也有將「月球橢圓軌道的不均勻視運動及其進動現象」模擬進圖中。

下兩圖則是按照真實的地球繞日與月球繞地的「離心率」所畫出的圖，可以看到兩個軌道都很接近正圓，不過為了方便讀者觀察，月球軌道的半長軸還是放大了不然會完全看不到。

上圖的地球運行靠近「近日點」，地球繞日的角速度較快，月球需多繞一些方能回到「朔」的相位，因此其天數相較下圖較長些。

上圖比較靠近「遠日點」，地球繞日的角速度較慢，月球花少一點點的時間便可回到「朔」的相位，因此可以看到此朔望月的天數較短些。

雖然有眾多影響「朔望月」長度的因素，但朔望月的長度不會長過30天，也不會短於29天，根據NASA的數據，目前所知最長的天數是29.84089天，最短則是29.26574天。因此照實際朔望月來排定月份的長度，天數始終會是29天或30天。


這篇文章中我們簡單介紹了一些會影響「朔望月」長度的因素，日後的文章我們會繼續介紹古代怎麼利用觀測的數值來修正「朔望月」的長度，進而採用「進朔」以及最終的「定朔」。

太陽運動 (3)：中心差

在【太陽運動 (2)：黃道與天球赤道，真近點角與平近點角】最後，我們做圖後發現了一個看似sine(正弦函數)的圖形，這也是【太陽運動 (1)：史書中暗藏的正弦函數】中我們意外發現史書中的數字所能畫出的圖形，以當時古代曆法的年代，當然不會知道這張圖代表的意義，但測量與天體運動的原理是不會改變的，我們來使用後代的數學來解釋為什麼看到了這樣子的圖形。

事實上，這張圖描述的即是近代天文物理學二體問題中有名的「中心差」(equation of the center)。

要推導接下來的式子其實步驟很多，以筆者的參考書籍【Methods of celestial mechanics】就花了$17$頁左右的篇幅，就科普文的來說不太適合，真要推導也只會變成抄書而已。筆者在此就簡單介紹幾個重要的步驟，以及會運用到的一些定理，若讀者有興趣可以直接前往閱讀。

我們的目的是要簡化「真近點角減平近點角」，但直接展開不容易，透過一些輔助會簡單得多。因此在介紹前，要先讓大家認識克卜勒方程式(Kepler's equation)，乍聽之下是大家熟知的克卜勒定律：橢圓軌道、角動量守恆、公轉周期平方與軌道半長軸立方成正比，但其實克卜勒方程式指的是另一條有名的方程式，也是一條與描述橢圓軌道有關的方程式：

為方便說明，地球軌道非真實比例

克卜勒在此引入了一個圓心O的輔助圓，假設在想像中的情況下行星以等速率圓周運動繞圓心O公轉，而當行星從「近日點」以等角速度行進至圖中的位置(圖中之「等角速度」)時，在相同時間內，若地球以按照克卜勒定律的方式運行，則會運行到圖中「地球」的位置。從地球向線段(O-近日點)做垂線並延伸至該輔助圓，可以得到點P。圖中的$\angle$地球-太陽-近日點稱為「真近點角」(true anomaly)，$\angle$等角速度-O-近日點稱為「平近點角」(mean anomaly)，$\angle$P-O-近日點則稱為「偏近點角」(eccentric anomaly)。

推導之後可得克卜勒方程式： \[ M = E - e \sin E \]

上式中的$M$是「平近點角」，$E$是「偏近點角」，$e$則是「離心率」即橢圓方程式：$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $ ，其中離心率即為 $ e = \sqrt{1-\frac{b^2}{a^2}} $。

這裡引入了一個「偏近點角」，透過偏近點角，將這些週期函數做傅立葉級數展開會比較容易些，同時我們也需要運用「真近點角$T$」與「偏近點角$E$」的關係：\[ \cos T = \frac{\cos E - e}{ 1 - e \cdot \cos E} \]

有了這幾個式子，我們可以對這些週期函數做傅立葉級數展開，即大家可能熟知的技巧： \[ \begin{align*} &f(x) = a_{0} + 2 \sum_{1}^{\infty} a_{p} \cos px + 2 \sum_{1}^{\infty} b_{p} \sin px \\ &a_{0} = \frac{1}{ 2\pi} \int_{0}^{2\pi} f(x) \,dx \\ &a_{p} = \frac{1}{ 2\pi} \int_{0}^{2\pi} f(x) \cos \,px \,dx \\ &b_{p} = \frac{1}{ 2\pi} \int_{0}^{2\pi} f(x) \sin \,px \,dx , p = +1, +2 ... \infty \\ \end{align*} \]

如果要繼續推導下去讀者可能會看得有點累，建議有興趣的讀者可以直接前往筆者的參考書籍【Methods of celestial mechanics】$60$頁至$76$頁查閱。 若展開到 $e^7$，偏近點角$E$可對平近點角$M$展開成： \[ \begin{align*} E= M &+ \left( e-\frac{1}{8}e^3 + \frac{1}{192}e^5 - \frac{1}{9216}e^7 \right) \sin M \\ &+ \left( \frac{1}{2}e^2 -\frac{1}{6}e^4 + \frac{1}{48}e^6 \right) \sin 2M + \left( \frac{3}{8}e^3 -\frac{27}{128}e^5 +\frac{243}{5120}e^7 \right) \sin 3M \\ &+ \left( \frac{1}{3}e^4 - \frac{4}{15}e^6 \right) \sin 4M + \left( \frac{125}{384}e^5 -\frac{3125}{9216}e^7 \sin 5M \right) \\ &+ \frac{27}{80} e^6 \sin 6M + \frac{16807}{46080}e^7 \sin 7M \\ \end{align*} \] 再根據偏近點角$E$與真近點角$T$的關係，最終真近點角$T$對平近點角$M$若展開到$e^7$則成： \[ \begin{align*} T = M &+ \left( 2e - \frac{1}{4}e^3 + \frac{5}{96}e^5 + \frac{107}{4608}e^7 \right) \sin M \\ &+ \left( \frac{5}{4}e^2 -\frac{11}{24}e^4 + \frac{17}{192}e^6 \right) \sin 2M + \left( \frac{13}{12}e^3 -\frac{43}{64}e^5 +\frac{95}{512}e^7 \right) \sin 3M \\ &+ \left( \frac{103}{96}e^4 - \frac{451}{480}e^6 \right) \sin 4M + \left( \frac{1097}{960}e^5 -\frac{5957}{4608}e^7 \sin 5M \right) \\ &+ \frac{1223}{960} e^6 \sin 6M + \frac{47273}{32256}e^7 \sin 7M \\ \end{align*} \]

因為真實的行星軌道的離心率都非常小接近0，因此上式中 $e^2$之後的數字都會非常小可以忽略不計，也就會變成： \[ T-M = 2e \sin M \] 即「真近點角減平近點角」會非常近似sine(正弦函數)，最大最小值皆為 $2e$。

為方便讀者想像，下圖是以假設地球公轉軌道為離心率0.833的軌道所做出的圖形：

因為離心率很接近1，這時候上面式子各e的次方項就不太能省略了，所以如果將「真近點角減平近點角」對時間做圖會畫出下面的圖形：

但地球真實軌道的離心率僅有0.0167086，很接近正圓，如下圖：

這時候$e^2$之後便能省略，也因此「真近點角減平近點角」對時間做圖就會畫出如上述所說的sine(正弦函數)的圖形了！

也可以看到最大最小值確實是$\pm 0.0167086 \times 2 =\pm 0.0334172 $。

這就是【太陽運動 (1)：史書中暗藏的正弦函數】中，所畫出的正弦函數的來源了！

花了不少時間，我們終於解惑了神祕的圖形是怎麼來的了，詳細的推導過程就請讀者們自行參閱參考書籍了，筆者列的參考書籍僅是其中一種推導過程，筆者看過各種不同的推導方式，當然最終結論都是相同的。

確認以及慢慢可以預測太陽運動的非等速率運動，對於曆法的制定也是非常重要的，除了顯而易見的節氣之外，朔望月也的長度也受此影響，不難想像，在近日點時的冬季，因為地球公轉稍快，月球要回到相同相位的時間需稍久些，因此對太陽運動有更多的認識後朔望月也終於可以慢慢改用「定朔」而非「平朔」了，這部分我們會在日後繼續說明。