古代怎麼推算朔日 (1)：概論

之前說明了農曆是怎麼定義一個月：每個月的初一是由朔日來定義，相鄰兩個朔日定義了一個月的長度，但朔日又要怎麼推算呢？夜晚看不見月亮的那一天？太粗糙了，而且跟節氣一樣，總不可能觀測完再宣告合朔時刻 (月亮走到地球與太陽之間的那一刻) 以及朔日，那個沒有人造衛星的年代，除非日食不然也沒辦法準確觀測合朔，總不能遇到日食的時候再宣布該日為初一，那沒有日食的月份該怎麼辦？跟節氣一樣，曆法中合朔總是要事先推算的，古代又是怎麼推算的呢？

其實計算方法跟推算二十四節氣很類似，但因為月球運行週期短比較容易觀測記錄，每個月長度不一很早就知道，所以推算各個月朔日的方式也慢慢改進 (平朔、進朔、定朔等)。這篇文章主要講解的是，含「冬至」那個月 (子月) 的朔日 (初一) 是怎麼推算的，這部分就不受校正每個月長度方法的影響，其餘的月份不同校正的算法我們還會在其他文章中慢慢解說。

因為文末驗證的關係，我們這裡用「大衍曆」來講解：

【新唐書卷二十八上志第十八上曆四上】

《開元大衍曆》演紀上元閼逢困敦之歲，距開元十二年甲子，積九千六百九十六萬一千七百四十算。

通法三千四十。
策實百一十一萬三百四十三。
揲法八萬九千七百七十三。

以策實乘積算，曰中積分。

以揲法去中積分，不盡曰歸餘之掛。以減中積分，為朔積分。如通法為日，去命如前，得天正經朔。

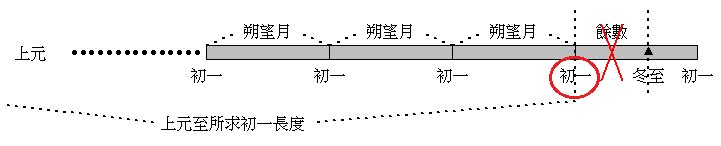
看起來很複雜，但跟之前一樣，這裡只有簡單的加減乘除，小學程度而已，只是因為文言看起來比較複雜。我們如果先將曆法中記載的部分擱一邊，直接看圖示會比較好懂。

我們要算的是某年冬至那個月的初一 (朔) 是哪一天。【二十四節氣 (4) ：如何推算冬至是未來的哪一天？】有提及，我們可以從提供的數據來算出上元到冬至共有幾天。而算出天數之後，可以再根據「朔望月」的長度，來得知總共過了幾個「朔望月」，因為「朔望月」與「回歸年」不是倍數的關係，除非剛好大循環到一段落，冬至點不會剛剛好就是「合朔時刻」，因此我們可以算出「冬至點」是「合朔」過了幾日。

也可以因此得知，上元到「欲求月之合朔時刻」共有幾天，再根據之前一樣的方法，除以$60$得到的餘數，我們便可得知該「朔日」以干支記日是哪一天，同樣也可從分數位得知合朔是哪一時刻。

回過頭來看史書中的記載：「通法」$3040$是一天切成幾等分，「策實」$1110343$是一個「回歸年」有幾個「通法」的等分，「揲法」$89773$是第一次在我們文章中出現，是一個「朔望月」有幾個「通法」的等分。「積算」$96961740$是上元到開元十二年剛過的那個年底冬至總共經過$96961740$個回歸年，即上元積年。 「以策實乘積算，曰中積分」，這是上元算到所求冬至的長度，在之前文章中已使用多次並有說明。

「以揲法去中積分，不盡曰歸餘之掛」，「中積分」(上元至冬至的長度) 反覆減去「揲法」(朔望月的長度)，剩下的數稱為「歸餘之掛」(所求朔至冬至的長度)，「歸餘之掛」其實就是「中積分」除以「揲法」的餘數。「以減中積分，為朔積分」，把算出的餘數從「中積分」(上元至冬至的長度)中減去，也就是上元至所求朔的長度 (朔積分)。

「通法為日」，上述長度是以「通法」即把一日分成$3040$等分為單位，所以最後「朔積分」還需再除以「通法」，就是上元至所求合朔時刻的「天數」，這裡「通法為日」的「日」不是天數、日期的意思，而是古代稱分數的分母為「日」。最後再把求出之天數除以$60$的餘數，便可得知以干支記日是哪一天了。

實際運算看看，大衍曆在開元十七年(西元$729$年)開始施行，我們來計算看看開元十八年(西元$730$年)年底的冬至那個月的合朔是什麼時刻：

根據最初曆書中的數字，可以知道大衍曆使用$\frac{1110434}{3040}=365 \frac{743}{3040}= 365.2444$天為一個回歸年的長度，朔望月的長度則是$\frac{89773}{3040}=29 \frac{1613}{3040}= 29.53059$天。計算的時候因為分母都是「通法」$3040$，所以最後再除以「通法」即可，上述圖示也省略「通法」。

如同之前文章所說，曆書中所指之積年，通常是算到前一年年底的冬至，所以曆書中的積算$96961740$是算到開元十一年(西元$723$年)年底冬至，我們要算的開元十八年(西元$730$年)，積算則是$96961747$年，有了這些數字便可以計算了：

中積分$=$策實乘積算：$1110343 \times 96961747 = 107660797049221 $

歸餘之掛 $=$ 中積分除以揲法的餘數：$107660797049221 \equiv 11257\ ( mod\ 89773) $

朔積分$=$ 中積分減去歸餘之掛： $107660797049221 - 11257 = 107660797037964 $

朔積分換算成以天數為單位：$\frac{107660797037964}{3040}=35414735867 \frac{2284}{3040}$

天正經朔，把天數用干支記日表示：$35414735867 \frac{2284}{3040} \equiv 47\frac{2284}{3040}\ ( mod\ 60) $

查表可知$47$為辛亥，所以開元十八年年底的十一月子月朔日即為辛亥日。

---

我們也一樣來從古籍中驗證，筆者再次從維基文庫中，找到了這篇王維的文章，用大文學家的作品來當驗證總是比較有感覺的：

【為崔常侍祭牙門姜將軍文】 維大唐開元二十五年歲次丁丑十一月辛未朔四日甲戌，左散騎常侍河西節度副大使攝御史中丞崔公，致祭於故姜公之靈：嗚呼！天子命我，建旗西門。帶甲十萬，鐵騎雲屯。橫挑強胡，飲馬河源。嗟爾勇健，表為牙門。牙門伊何？全齊大族。四方有事，誓死鳴轂。前有血刃，後有飛鏃。其氣益振，大呼馳逐。翩翩白馬，象弧雕服。戈春其喉，矢注其目。嗚呼！天下無事，今上好文。爾有餘勇，莫敢邀勳。腰鞬白首，蹉跎塞雲。死於裨將，誰統前軍？家本秦人，靈車東騖。長天積雪，邊城欲暮。麾下行哭，前旌抗路。身有寶劍，不佩而去。轅有代馬，悲鳴跼顧。嗚呼！我誡軍吏，令送爾歸。既素我服，亦朱其衣。黠虜未滅，壯士長辭。牢禮以祭，太息歔欷。尚饗。

所以我們要算的是開元二十五年年底十一月的朔日，而根據王維文章中第一句，該日是「辛未日」，讓我們來驗證看看吧：

開元二十五年用的即為上述講解中的大衍曆，所以直接引用上面的數字即可。上面算到開元十八年年底冬至，再經過了七年，積算為$96961747+7$。

中積分$=$策實乘積算：$1110343 \times (96961747+7) = 107660804821622 $

歸餘之掛 $=$ 中積分除以揲法的餘數：$107660804821622 \equiv 63180\ ( mod\ 89773) $

朔積分$=$ 中積分減去歸餘之掛： $107660804821622 - 63180 = 107660804758442 $

朔積分換算成以天數為單位：$\frac{107660804758442}{3040}=35414738407 \frac{1162}{3040}$

天正經朔，把天數用干支記日表示：$35414738407 \frac{1162}{3040} \equiv 7\frac{1162}{3040}\ ( mod\ 60) $

餘數為$7$，查表可知為「辛未」，跟王維寫的一樣！

相信大家能更熟悉以前是怎麼推算朔日，不過這種算法只適用於推算「冬至月」的朔日，因為「朔望月」僅為一平均值，實際月的運行會受到月球軌道與地球繞日軌道的影響，因此推算其他各月朔日的方式也隨著時間慢慢演進，從最早的平朔，各個月直接累加平均朔望月的長度即可，到之後進朔、定朔的方式，這些在以後還會慢慢說明。另外，上述計算法其實也有更簡明的算法，這些也都有在曆書中記載，也會在之後慢慢講解。