閏月是怎麼決定的 (2)：太初曆

在之前【閏月是怎麼決定的 (1)：概論】文章中提及過，從有明確史料的太初曆 (西元前$104$年 - 西元$4$年) 開始，農曆便是採用「無中置閏」的方式來決定閏月，但其實這只是大原則而已，在麟德曆 (西元$666$年 - 西元$728$年) 之前一直還採用「閏周」的方式來決定閏月。

什麼是「閏周」？閏周就是大家耳熟能詳的「$19$年$7$閏」或是之後祖沖之曾採用過的「$391$年$144$閏」，其中「$19$年$7$閏」的「$19$年」的$19$稱為章歲，「$7$閏」的$7$稱為章閏。

在古代最初採用平氣平朔的曆法時，計算閏月的方式相對簡單。在本篇中主要要講解的是，在太初曆當時是如何使用「閏周」的方式來決定閏月的。

先把古書放一邊，了解一下基本的概念，太初曆使用的是$19$年$7$閏，也就是$235$個農曆月中有$7$個是閏月，數字的由來在之前【閏月是怎麼決定的 (1)：概論】中有提及：

因為一個回歸年 $365.2422$ 天，若經過 $19$ 年，$365.2422 \times 19 = 6939.602$，其天數跟 $235$ 個朔望月 $29.5306 \times 235 = 6939.691$ 的天數非常接近，而 $235 = 12 \times 19 + 7$，也就是在這$19$年間，每年除了$12$個月之外，如果在$19$年間另外加入$7$個月的話，回歸年與朔望月便會形成一個很接近的循環，在古代曆法中，$19$ 便為一個「章」。

根據這幾個數字我們可以知道，如果把這$235$個農曆月平均分在$19$個回歸年間，一個回歸年共有$\frac{235}{19}=12\frac{7}{19}=12.368$個月左右，以一年正常$12$個月來看，每一年會多$\frac{7}{19}=0.368$個月左右，相當於每年會累積$\frac{7}{19}$個閏月，當這個月份累積超過$1$的時候，便是放置閏月的時候，再根據無中置閏的原則來看什麼時候是閏月。

這個累積閏月的基準點，跟之前一樣同樣是從「上元」開始累積，假設從上元開始經過了$2$個回歸年到了該年冬至，則共有 $\frac{235}{19} \times 2 = 24 \frac{14}{19}$個月，分數的部分即是閏月累積的月，因為還沒有超過$\frac{19}{19}$，目前還不用置閏，但可預期接下來的回歸年會再累積 $\frac{7}{19}$個閏月，分數的部分就會大於$1$了，所以我們知道接下來的回歸年會需要多個閏月。因為每年都是累積 $\frac{7}{19}$個閏月，當算到前一個回歸年累積的閏月超過 $\frac{12}{19}$個月時，接下來的一年累積的月份就會大於$1$，也就需要置閏了。

來看史書中的記載，太初曆的部分沒有仔細描述，不過由太初曆稍加改編的三統曆 (西元$5$年 - 西元$84$年) 寫得很清楚：

【漢書卷二十一律曆志第一】
統母日法八十一。
閏法十九，因為章歲。
章月二百三十五。
月法二千三百九十二。
周天五十六萬二千一百二十。
章中二百二十八。
推天正，以章月乘人(入)統歲數，盈章歲得一，名曰積月，不盈者名曰閏餘。閏餘十二以上，歲有閏。

括號的部分是因為史書傳抄之後版本不同的關係。裡面很多的數字都在之前的不同文章中曾提及，在此就不再重覆解釋。

前段曾提過實際的$19$個回歸年的天數與$235$個朔望月的天數非常接近，但只是非常接近並不相等，而在早期使用閏周的曆法，如這裡的太初曆/三統曆，如果我們仔細看其使用的數字，回歸年的長度與朔望月的長度是設計成真的過了$19$個回歸年就是一個大循環。以曆書中的數字來看，太初曆/三統曆使用的回歸年長度是$\frac{562120}{1539}=365\frac{385}{1539}=365.2502$天，而朔望月的長度是$\frac{2392}{81}=29\frac{43}{81}=29.53086$天，$19$個回歸年的長度則是$\frac{562120}{1539} \times 19 = \frac{562120}{81}$天，$235$個朔望月也剛剛好是$\frac{2392}{81} \times 235 = \frac{562120}{81}$天，數字是設計好的，也因為這樣，在計算閏月的時候會更簡單一些。

以章月乘人統歲數，盈章歲得一，名曰積月，不盈者名曰閏餘。「人統歲數」即「上元積年」，這其實就是上述所說的，如果要算某年(上元積年共$N$年)是否要置閏，「章月乘以上元積年除以章歲」$235 \times N \div 19 = \frac{235}{19} \times N = 積月 + \frac{閏餘}{19}$。閏餘十二以上，歲有閏，如上述所說，如果分數的部分$\geq \frac{12}{19}$，則接下來的回歸年累積閏月一定會$\geq 1$，所以「閏餘十二以上，歲有閏」。

---

至於哪一個月份要置閏呢？

置閏的原則是無中氣的月份置閏，$19$個回歸年共有$12 \times 19=228$個中氣，又因為$19$個回歸年需置7個閏月，所以平均每個中氣會累積$\frac{7}{228}個閏月$，亦即每過一個朔望月，該月的中氣會再離該月的朔更遠一些，即$\frac{7}{228}$個月。

或是我們可以用另個方式來理解，假設最初合朔時刻與中氣點的時刻是相同的，經過一個朔望月也就是$29\frac{43}{81}=29.53086$天，但下一個中氣則是$365\frac{385}{1539} \times \frac{1}{12}= 30.43751$天之後，所以每過一個朔望月，中氣會遠離朔$(365\frac{385}{1539} \times \frac{1}{12}-29\frac{43}{81})$天，即 $$\begin{align*} \frac{562120}{1539}\times \frac{1}{12} -\frac{2392}{81} &= \frac{2392 \times 235}{81 \times 19 } \times \frac{1}{12}- \frac{2392}{81} \\ &= \frac{2392}{81} \times (\frac{235}{19 \times 12} - \frac{19 \times 12}{19 \times 12} )\\ &= \frac{2392}{81} \times \frac{235-228}{228}\\ &= \frac{2392}{81} \times \frac{7}{228} \end{align*}$$ ， 也就是一個朔望月的長度乘以$\frac{7}{228}$，即上述說的$\frac{7}{228}$個月。

數字這麼漂亮當然是因為設計過的所以必然如此。如果要知道某年的第$k$個中氣是否會需要閏月，根據前段所述，我們知道算到該年冬至累積的「閏餘」的算法是$235 \times N \div 19 = \frac{235}{19} \times N = 積月 + \frac{閏餘}{19}$。事實上，這個$\frac{閏餘}{19}$的部分，跟前一篇文章的「歸餘之掛」的概念是非常類似的，不過因為最早的曆法有採取閏周，數字特別設計過，算起來不像前一篇【古代怎麼推算朔日 (1)：概論】所述相對複雜。

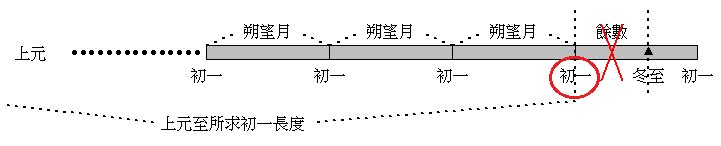
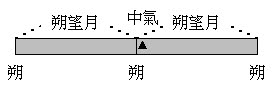
也就是這裡的閏餘，其實就是該月朔到冬至的長度。那我們要計算的是第$k$個中氣，所以閏餘的部分要繼續累加到第$k$個中氣，也就是$\frac{閏餘}{19}+\frac{7}{228} \times k = \frac{閏餘\times 12}{19 \times 12} + \frac{7}{228} \times k = \frac{閏餘 \times 12 + 7k}{228}$，即經過了$k$個中氣之後，中氣點的時刻距離該月合朔時刻的長度 (以月為單位)，那現在問題就很簡單了，如果這個數字小於$1$，那我們知道該中氣離朔的距離還不到一個朔望月的長度，如果再算到下一個月，這個值大於$1$的話，也就是如下圖所示：

其中有一個朔望月不含中氣，那就可以知道這裡要置閏了。範例可見下圖：

此時不含「中氣」的那個月便會是個閏月。

再來看曆書是怎麼寫的：

【漢書卷二十一律曆志第一】
推閏餘所在，以十二乘閏餘，加七(十)得一。盈章中，數所得，起冬至，算外，則中至終閏。盈中氣在朔若二日，則前月閏也。

「十二乘閏餘加七，除以章中」，「章中」就是一個章($19$個回歸年)含有的中氣數，也就是曆書中有寫出的$228$。這一段其實就是$\frac{閏餘 \times 12 + 7k}{228}$。

從冬至開始算起，如果有一個朔望月不含中氣，「則中至終閏」，就是要放置閏月的時候了。此時，那個在閏月後出現的中氣稱為「盈中氣」，因為兩個中氣相隔的長度僅$30$多天，所以這個「盈中氣」一定是出現在初一或初二，也就是「在朔若二日」。

最後，「則前月閏也」，不過如果真的照這個算法的話，其實會有一點小問題，譬如假設「穀雨」這個中氣的中氣點是在該月初一下午$1$點，該月合朔時刻是在初一下午$2$點，次月合朔時刻是在初一上午$7$點，「小滿」這個中氣的中氣點是在次月初一上午$8$點，如下圖所示：

也就是說，計算的結果會是該月朔至次月朔的這段期間內沒有「中氣」，但是因為「穀雨」的中氣點是在初一，所以在曆法的訂定上「該月」含有「穀雨」這個「中氣」，這樣就不能當閏月了。事實上從該月往回查閱通常一到兩個月可以找到無中氣的月份，也就是「則前月閏也」，這裡的「前月」不是「前一個月」，而是「之前的某個月」。所以用這種計算法，還不一定能真的直接確定閏月的位置，不過已經可以大致推算出來了。

這種計算法之後還有曆法曾使用過，但是大多數的曆書都是採用其他的算法，這部分我們在之後的文章還會繼續說明。





參考文獻：中國數理天文學。2008年。曲安京著。科學出版社。

古代怎麼推算朔日 (1)：概論

之前說明了農曆是怎麼定義一個月：每個月的初一是由朔日來定義，相鄰兩個朔日定義了一個月的長度，但朔日又要怎麼推算呢？夜晚看不見月亮的那一天？太粗糙了，而且跟節氣一樣，總不可能觀測完再宣告合朔時刻 (月亮走到地球與太陽之間的那一刻) 以及朔日，那個沒有人造衛星的年代，除非日食不然也沒辦法準確觀測合朔，總不能遇到日食的時候再宣布該日為初一，那沒有日食的月份該怎麼辦？跟節氣一樣，曆法中合朔總是要事先推算的，古代又是怎麼推算的呢？

其實計算方法跟推算二十四節氣很類似，但因為月球運行週期短比較容易觀測記錄，每個月長度不一很早就知道，所以推算各個月朔日的方式也慢慢改進 (平朔、進朔、定朔等)。這篇文章主要講解的是，含「冬至」那個月 (子月) 的朔日 (初一) 是怎麼推算的，這部分就不受校正每個月長度方法的影響，其餘的月份不同校正的算法我們還會在其他文章中慢慢解說。

因為文末驗證的關係，我們這裡用「大衍曆」來講解：

【新唐書卷二十八上志第十八上曆四上】

《開元大衍曆》演紀上元閼逢困敦之歲，距開元十二年甲子，積九千六百九十六萬一千七百四十算。

通法三千四十。
策實百一十一萬三百四十三。
揲法八萬九千七百七十三。

以策實乘積算，曰中積分。

以揲法去中積分，不盡曰歸餘之掛。以減中積分，為朔積分。如通法為日，去命如前，得天正經朔。

看起來很複雜，但跟之前一樣，這裡只有簡單的加減乘除，小學程度而已，只是因為文言看起來比較複雜。我們如果先將曆法中記載的部分擱一邊，直接看圖示會比較好懂。

我們要算的是某年冬至那個月的初一 (朔) 是哪一天。【二十四節氣 (4) ：如何推算冬至是未來的哪一天？】有提及，我們可以從提供的數據來算出上元到冬至共有幾天。而算出天數之後，可以再根據「朔望月」的長度，來得知總共過了幾個「朔望月」，因為「朔望月」與「回歸年」不是倍數的關係，除非剛好大循環到一段落，冬至點不會剛剛好就是「合朔時刻」，因此我們可以算出「冬至點」是「合朔」過了幾日。

也可以因此得知，上元到「欲求月之合朔時刻」共有幾天，再根據之前一樣的方法，除以$60$得到的餘數，我們便可得知該「朔日」以干支記日是哪一天，同樣也可從分數位得知合朔是哪一時刻。

回過頭來看史書中的記載：「通法」$3040$是一天切成幾等分，「策實」$1110343$是一個「回歸年」有幾個「通法」的等分，「揲法」$89773$是第一次在我們文章中出現，是一個「朔望月」有幾個「通法」的等分。「積算」$96961740$是上元到開元十二年剛過的那個年底冬至總共經過$96961740$個回歸年，即上元積年。 「以策實乘積算，曰中積分」，這是上元算到所求冬至的長度，在之前文章中已使用多次並有說明。

「以揲法去中積分，不盡曰歸餘之掛」，「中積分」(上元至冬至的長度) 反覆減去「揲法」(朔望月的長度)，剩下的數稱為「歸餘之掛」(所求朔至冬至的長度)，「歸餘之掛」其實就是「中積分」除以「揲法」的餘數。「以減中積分，為朔積分」，把算出的餘數從「中積分」(上元至冬至的長度)中減去，也就是上元至所求朔的長度 (朔積分)。

「通法為日」，上述長度是以「通法」即把一日分成$3040$等分為單位，所以最後「朔積分」還需再除以「通法」，就是上元至所求合朔時刻的「天數」，這裡「通法為日」的「日」不是天數、日期的意思，而是古代稱分數的分母為「日」。最後再把求出之天數除以$60$的餘數，便可得知以干支記日是哪一天了。

實際運算看看，大衍曆在開元十七年(西元$729$年)開始施行，我們來計算看看開元十八年(西元$730$年)年底的冬至那個月的合朔是什麼時刻：

根據最初曆書中的數字，可以知道大衍曆使用$\frac{1110434}{3040}=365 \frac{743}{3040}= 365.2444$天為一個回歸年的長度，朔望月的長度則是$\frac{89773}{3040}=29 \frac{1613}{3040}= 29.53059$天。計算的時候因為分母都是「通法」$3040$，所以最後再除以「通法」即可，上述圖示也省略「通法」。

如同之前文章所說，曆書中所指之積年，通常是算到前一年年底的冬至，所以曆書中的積算$96961740$是算到開元十一年(西元$723$年)年底冬至，我們要算的開元十八年(西元$730$年)，積算則是$96961747$年，有了這些數字便可以計算了：

中積分$=$策實乘積算：$1110343 \times 96961747 = 107660797049221$

歸餘之掛 $=$ 中積分除以揲法的餘數：$107660797049221 \equiv 11257\ ( mod\ 89773)$

朔積分$=$ 中積分減去歸餘之掛： $107660797049221 - 11257 = 107660797037964$

朔積分換算成以天數為單位：$\frac{107660797037964}{3040}=35414735867 \frac{2284}{3040}$

天正經朔，把天數用干支記日表示：$35414735867 \frac{2284}{3040} \equiv 47\frac{2284}{3040}\ ( mod\ 60)$

查表可知$47$為辛亥，所以開元十八年年底的十一月子月朔日即為辛亥日。

---

我們也一樣來從古籍中驗證，筆者再次從維基文庫中，找到了這篇王維的文章，用大文學家的作品來當驗證總是比較有感覺的：

【為崔常侍祭牙門姜將軍文】 維大唐開元二十五年歲次丁丑十一月辛未朔四日甲戌，左散騎常侍河西節度副大使攝御史中丞崔公，致祭於故姜公之靈：嗚呼！天子命我，建旗西門。帶甲十萬，鐵騎雲屯。橫挑強胡，飲馬河源。嗟爾勇健，表為牙門。牙門伊何？全齊大族。四方有事，誓死鳴轂。前有血刃，後有飛鏃。其氣益振，大呼馳逐。翩翩白馬，象弧雕服。戈春其喉，矢注其目。嗚呼！天下無事，今上好文。爾有餘勇，莫敢邀勳。腰鞬白首，蹉跎塞雲。死於裨將，誰統前軍？家本秦人，靈車東騖。長天積雪，邊城欲暮。麾下行哭，前旌抗路。身有寶劍，不佩而去。轅有代馬，悲鳴跼顧。嗚呼！我誡軍吏，令送爾歸。既素我服，亦朱其衣。黠虜未滅，壯士長辭。牢禮以祭，太息歔欷。尚饗。

所以我們要算的是開元二十五年年底十一月的朔日，而根據王維文章中第一句，該日是「辛未日」，讓我們來驗證看看吧：

開元二十五年用的即為上述講解中的大衍曆，所以直接引用上面的數字即可。上面算到開元十八年年底冬至，再經過了七年，積算為$96961747+7$。

中積分$=$策實乘積算：$1110343 \times (96961747+7) = 107660804821622$

歸餘之掛 $=$ 中積分除以揲法的餘數：$107660804821622 \equiv 63180\ ( mod\ 89773)$

朔積分$=$ 中積分減去歸餘之掛： $107660804821622 - 63180 = 107660804758442$

朔積分換算成以天數為單位：$\frac{107660804758442}{3040}=35414738407 \frac{1162}{3040}$

天正經朔，把天數用干支記日表示：$35414738407 \frac{1162}{3040} \equiv 7\frac{1162}{3040}\ ( mod\ 60)$

餘數為$7$，查表可知為「辛未」，跟王維寫的一樣！

相信大家能更熟悉以前是怎麼推算朔日，不過這種算法只適用於推算「冬至月」的朔日，因為「朔望月」僅為一平均值，實際月的運行會受到月球軌道與地球繞日軌道的影響，因此推算其他各月朔日的方式也隨著時間慢慢演進，從最早的平朔，各個月直接累加平均朔望月的長度即可，到之後進朔、定朔的方式，這些在以後還會慢慢說明。另外，上述計算法其實也有更簡明的算法，這些也都有在曆書中記載，也會在之後慢慢講解。

杜甫的算術...... 非常厲害？秋分是什麼時候

「國破山河在，城春草木深」，「劍外忽傳收薊北，忽聞涕淚滿衣裳」，詩聖杜甫的詩大家不陌生，許多詩也收錄為國文課文讓我們不得不熟悉。杜甫當然不是只會寫詩，也有許多文章傳於後世。眾多文章裡，杜甫在【唐興縣客館記】中，最末留下了讓人難以參透的一句：

中興之四年，王潛為唐興宰，修厥政事。始自鰥寡惸獨，而和其封內，非侮循循，不畏險膚，而行而一。諮於官屬、於群吏、於眾庶曰：「邑中之政，庶幾繕完矣。惟賓館上漏下濕，吾人猶不堪其居，以容四方賓，賓其謂我何？改之重勞，我其謂人何？」咸曰：「誕事至濟厥載，則達觀於大壯。」作之閈閎，作之堂構，以永圖崇高廣大，逾越傳舍，通梁直走，嵬將墜壓，素柱上承，安若泰山，兩傍序開，發泄霜露，潛靜深矣。步櫩復霤，萬瓦在後，匪丹雘為實，疏達為迥廊，南注又為覆廊，以容介行人，亦如正館，制度小劣。直左階而東，封殖修竹茂樹；挾右階於南，環廊又注，亦可以行步，風雨不易。謀而集事，邑無妨工，亦無匱財，人不待子來，定不待方中矣。宿息井樹，或相為賓，或與之毛，天子之使至，則曰邑有人焉，某無以栗階。州長之使至，則曰某非敢賓也，子無所用俎。四方之使至，則曰子貺某多矣，敢辭贄。或曰明府君之侈也，何以為人？皆曰我公之為人也，何以侈！子徒見賓館之近夫厚，不知其私室之甚薄，器物未備，力取諸私室，人民不知賦斂。乃至於館之醯醢闕，出於私廚；使之乘駟闕，辦於私廄。君豈為亭長乎？是躬親也，若館宇不修，而觀台榭是好，賓至無所納其車，或浩蕩無所措手足，獲高枕乎？其誰不病吾人矣？疵瑕忽生，何以為之？是道也施捨，不幾乎先覺矣？杜之友朋歎曰：「美哉！，是館也成，人不知，人不怒，廨署之福也。府君之德也。」府君曰：「古有之也，非吾有也，余何能為？是亦前州府君崔公之命也，余何能為！」是日辛丑歲秋分，大餘二，小餘二千一百八十八，杜氏之老記已。

呃，這是什麼？兩個數字，$2$、$2188$？杜甫密碼？

這句子考倒了後代千餘年，為其作注者，有的不知所措胡言亂語，有的認輸，這到底是什麼密碼？

杜甫 (圖片來源：Wikipedia)

---

是日辛丑歲秋分，大餘二，小餘二千一百八十八，杜氏之老記已。

秋分、大餘、小餘？

初次接觸這幾個名詞數字的朋友可能會一頭霧水，但讀過上兩篇【二十四節氣 (4) ：如何推算冬至是未來的哪一天？】【二十四節氣 (5) ：如何推算二十四節氣是未來的哪一天？】的讀者，可能會意識到，這個該不會是在推算節氣吧？杜甫？你？

簡單複習一下：上兩篇提及了，唐代當時推算節氣的方法是利用上元積年推算出冬至，再累加天數至欲求得之節氣，如冬至到秋分過了$18$個節氣，亦即過了$\frac{18}{24}$個回歸年，再根據當時推算出的常數便可計算出。

下面考據可能會有點繁瑣，懶得看的話跳過沒關係，直接欣賞數字之美就可以了！

【唐興縣客館記】寫於「辛丑年」。杜甫生於西元$712$年，卒於$770$年，過世時不到$60$歲，所以人生中只會有一個辛丑年，簡單查詢可知應是唐肅宗上元二年(西元$761$年)。這時期根據史書的記載： 【新唐書卷二十七下 志第十七下 曆三下】至肅宗時，山人韓穎上言《大衍曆》或誤。帝疑之，以穎為太子宮門郎，直司天臺。又損益其術，每節增二日，更名《至德曆》，起乾元元年用之，訖上元三年。 乾元元年(西元$758$年)至上元三年(西元$762$年)應該是改「大衍曆」(西元$729$年 - 西元$758$?年)而使用「至德曆」，但史書中並無記載「至德曆」使用的相關常數。 【新唐書卷二十九 志第十九 曆五】寶應元年六月望戊夜，月蝕三之一。官曆加時在日出後，有交，不署蝕。代宗以《至德曆》不與天合，詔司天臺官屬郭獻之等，復用《麟德》元紀，更立歲差，增損遲疾、交會及五星差數，以寫《大衍》舊術。上元七曜，起赤道虛四度。帝為制序，題曰《五紀曆》。 短短幾年後，寶應元年 (即上元三年，西元$762$年) 覺得「至德曆」不好再改曆成「五紀曆」，改曆的結果還有參考「大衍曆」前一個「麟德曆」(西元$666$年 - 西元$728$年)。【唐興縣客館記】寫於上元二年 (西元$761$年)，這個年代應該要使用哪個曆我們這裡先不討論有點複雜，似乎應該是「至德曆」(西元$758$年 - 西元$762$年) 但「至德曆」啟用年限短而且之後改曆反而參考更早之前的曆法，在當時或許已知不準而有黑歷史之感，又或許杜甫當時被貶至蜀沒能來得及取得最新「至德曆」的數據。因為要算出這些數字算到剛剛好非常困難，如果數字一樣幾乎可以肯定是照所使用曆法的計算。而根據測試的結果直接透露結論，我們拿大衍曆 (西元$729$年 - 西元$762$?年)來計算吧！ 根據【新唐書卷二十八上 志第十八上 曆四上】： 《開元大衍曆》演紀上元閼逢困敦之歲，距開元十二年甲子，積九千六百九十六萬一千七百四十算。 以策實乘積算，曰中積分。盈通法得一，為積日。爻數去之，餘起甲子算外，得天正中氣。凡分為小餘，日為大餘。加三元之策，得次氣。 通法三千四十。 策實百一十一萬三百四十三。 三元之策十五，餘六百六十四，秒七。 上元到開元十二年(西元$724$年)共$96961740$年，而到了上元二年 (西元$761$年) 又過 $37$ 年。通法 $3040$，策實 $1110343$。

需要用到的數字都出現了，詳細的解釋上一篇有介紹，歡迎前往複習，或是直接往下單純欣賞漂亮的數字，既然【唐興縣客館記】最末句寫了「是日辛丑歲秋分」，那來算看看上元二年辛丑年 (西元$761$年) 的秋分 (冬至過後的第$18$個節氣) 是什麼時刻吧！

$\frac{1110343}{3040} = 365.2444$ 是該曆法一個回歸年的天數。

上元至上元二年 (西元$761$年) 剛過的冬至共有的天數，加上該冬至到秋分的天數

$$\begin{align*} &= \frac{1110343 \times (96961740+37)}{3040} + \frac{1110343}{3040} \times \frac{18}{24} \\ &= \frac{107660830359511}{3040} + \frac{19986174}{72960} = 35414747102.7198181152 \end{align*}$$

也就是算到上元二年的秋分共有$35414747102.7198181152$天，那除以$60$的餘數中的「大餘」和「小餘」便可以知道那一年的秋分以干支記日是哪一天，也可以知道準確的時刻了！

$35414747102.7198181152 \equiv 2.7198181152\ ( mod\ 60)$

小數的部分會用分母為$3040$的分數表示，所以：

$0.7198181152 \times 3040 = 2188.247$

因此算到秋分的餘數是 $2 \frac{2188}{3040}$。

使用小數只是方便計算，當時應該會使用類似分數的計算方式。 以下是現代分數的算式供參考： 曆書中有附上三元之策$15 \frac{664+ \frac{7}{24}}{3040}$，即$\frac{1110343}{3040} \times \frac{1}{24}$ ，欲知轉變過程可看上一篇。 $\frac{1110343 \times (96961740+37)}{3040} + \frac{1110343}{3040} \times \frac{1}{24} \times 18$ $= \frac{107660830359511}{3040} + 15 \frac{664+ \frac{7}{24}}{3040} \times 18$ $= 35414746828 \frac{2391}{3040} +15 \times 18 + \frac{664 \times 18 + \frac{7 \times 18 }{24}}{3040}$ $= 35414746828 \frac{2391}{3040} +270 + \frac{11952 + \frac{126 }{24}}{3040}$ $= 35414747098 \frac{2391}{3040} + \frac{11957 \frac{6 }{24}}{3040}$ $= 35414747098 \frac{2391}{3040} + \frac{3 \times 3040 +2837 + \frac{6 }{24}}{3040}$ $= 35414747098 \frac{2391}{3040} +3 + \frac{2837 + \frac{6 }{24}}{3040}$ $= 35414747101 \frac{2391}{3040} + \frac{2837 + \frac{6 }{24}}{3040}$ $= 35414747101 \frac{5228 + \frac{6 }{24}}{3040}$ $= 35414747102 \frac{2188 + \frac{6 }{24}}{3040}$ $35414747102 \frac{2188 + \frac{6 }{24}}{3040} \equiv 2 \frac{2188 + \frac{6 }{24}}{3040} ( mod\ 60)$

大餘$2$，小餘$2188$...！？這不就是杜甫記下的內容嗎？

杜老先生你在算秋分點！？大餘$2$是指該日以干支記日是甲子日後兩天，也就是丙寅日。小餘$2188$是指當一天切成$3040$等分時，在$2188$那一時刻。

這個是杜甫自己算的或是不知道哪裡抄來的我們就無法得知了，當時民間拿到的月曆年曆上會不會特別寫這個已經無法考證，但連現代的月曆都不太會寫，知道是哪一天已經很夠了，一般老百姓沒有必要知道秋分點是在什麼時刻啊。

筆者簡單查詢了文獻，古書中還有寫過「大餘小餘」的除了曆法相關書籍之外，暫時只查到宋代李石的大成井記，或是清代施鴻保的閩雜記有提及虞紹祖為重建樓作記亦曾記下，除此之外暫時還沒發現，不過筆者計算的結果李石好像有算錯？李石一生中所有的節氣似乎都不是這樣的大餘小餘？至於後者清代時已採定氣，上述計算方式倒已不適用，比較可能是查資料而來？所以可能一般月曆年曆不會特別標注這個？

這當然不是很難的數學只是四則運算，算術層級而已，但因位數有點多其實有點繁瑣......

筆者原先想筆算試試的，算沒幾秒鐘就覺得為什麼要浪費自己的美好生命在這上面。現代人要算這個也不是真的那麼容易，才沒幾年之前智慧型手機還沒問世時，如果手邊只有陽春型計算機，會因為位數過多而算不出來，靠電腦的幫忙則容易得多，現在則因為手機的計算機app，可能簡單多了。

可是杜甫先生你還真的算對了！？

雖然杜甫得到了正確答案，一個正常人再怎樣也不太會在記下日期的時候刻意這樣寫。今年 (西元$2020$年) 秋分點的時刻根據氣象局網頁是在臺灣時間$9$月$22$日$21$時$31$分，一個再文青的現代人，如果真的在秋分當日寫了篇文章，頂多寫個「寫於秋分」之類的，不會把秋分點的時間記上去吧？阿又不是寫文章的時間點，那是「秋分點」啊，而且要做作到這種程度還要刻意去查閱資料才能知道那準確的時間點，如果有人這樣做真無法想像那個人腦袋在想什麼。

可是一千多年前的詩聖杜甫杜老先生，不知道是自己計算的結果或是心血來潮想到這件事還不知去哪查閱後，就寫上去了？這絕對不可能是杜老先生寫文章的確切時間點，因為$2188$的分母是$3040$，杜老先生寫文章時還準備著一個日常生活中不太可能存在的$3040$等分計時裝置，然後刻意剛好在秋分點的時候寫了這篇文章。不可能的啦。這只是專指秋分點的時刻。

杜先生啊，呃，這樣是不是有點假掰？

---

後代有許多人幫其作註：

「朱注漢律厯志推正月朔以月法乘積月盈日法得一名曰積日不盈者名曰小餘小餘三十八以上其月大積日盈六十除之不盈者名曰大餘。姚江黃百家曰日法萬分毎刻百分毎日百刻總得萬分萬分以上為大餘日數也萬分以下為小餘時刻數也杜記蓋謂秋分後二日之二十餘刻耳。又曰漢厯所謂盈六十除之者六十即六十甲子名。旬周又名紀法滿紀者必去之以不滿紀者為主」

「朱」注的朱是明末清初的學者朱鶴齡，開頭就寫「漢律曆志」的推算法，雖然推算法除了數據外到唐代沒什麼改變，不過這個引用還是太過時了，平常投稿學術期刊，引用文獻稍微過時了幾年就會被二號審稿者刁，這個甚至過時幾百年了，而且後半段也沒寫什麼就是湊湊字數而已。姚江黃百家(黃宗羲之子)，是明末清初的曆法學家，「杜記蓋謂秋分後二日之二十餘刻耳」，沒有啊黃先生，杜甫不是這樣寫的啊裝什麼懂，身為曆法學家，不親自算算也不要隨便寫啊。

乾隆年間楊倫也曾為杜甫著作作注(讀書堂杜工部文註解二卷，pdf檔第$34$頁)，楊倫就誠實直白多了「末大餘小餘即觀朱釋亦未明」：大餘小餘朱鶴齡你的注在寫啥還是看不懂啦。

古代人遇到不會的事物會做的事跟現代人一樣，亂掰就對了，資訊流通沒那麼快，隨便講講也不會馬上被發現。愛寫嘛你們，過幾百年後就被發現了吧你看看你。

看了那麼多後代人裝懂又不懂，相較之下杜甫先生輕易地掌握曆算並算出了正確答案，雖然不一定是自己算的，也可能是別人算完再抄答案，但肯抄也暗示著自己了解這些數字的含意。既然已經無法考證誰算的，且讓我們浪漫一下，把計算的榮耀歸於杜甫吧。

亞洲人什麼數學不好，算術最好了！大文豪一千多年前就是這樣了啊……

古代非常厲害的人事物眾多，像是關公的青龍刀、蘇軾的東坡肉。在這長長的清單中，我們又可以多加一條，「杜甫的算術非常厲害」！

關公的青龍刀非常厲害。(圖片來源：網路)

蘇軾的東坡肉非常厲害。(圖片來源：Wikipedia)

作者：阿曆。作於西元$2020$年庚子年秋分前幾天。當然不是秋分點的那一刻。





參考文獻：謝思煒。杜甫詩文中的曆法問題。傅璇琮先生八十壽慶論文集。中華書局。2012年。

二十四節氣 (5) ：如何推算二十四節氣是未來的哪一天？

在上一篇文章中推算出了冬至日子與時刻，而為了架構整部曆法，二十四個節氣都非常重要，那其他節氣該怎麼推算？

周髀算經裡就有描述在不同節氣時測量正午的晷影。

周髀長八尺，夏至之日晷一尺六寸。 凡八節二十四氣，氣損益九寸九分六分分之一。冬至晷長一丈三尺五寸，夏至晷長一尺六寸。問次節損益寸數長短各幾何？ 冬至晷長丈三尺五寸， 小寒丈二尺五寸，小分五。 大寒丈一尺五寸一分，小分四。 立春丈五寸二分，小分三。 雨水九尺五寸三分，小分二。 啟蟄八尺五寸四分，小分一。 春分七尺五寸五分。 清明六尺五寸五分，小分五。 穀雨五尺五寸六分，小分四。 立夏四尺五寸七分，小分三。 小滿三尺五寸八分，小分二。 芒種二尺五寸九分，小分一。 夏至一尺六寸。 小暑二尺五寸九分，小分。 大暑三尺五寸八分，小分二。 立秋四尺五寸七分，小分三。 處暑五尺五寸六分，小分四。 白露六尺五寸五分，小分五。 秋分七尺五寸五分，小分一。 寒露八尺五寸四分，小分一。 霜降九尺五寸三分，小分二。 立冬丈五寸二分，小分三。 小雪丈一尺五寸一分，小分四。 大雪丈二尺五寸，小分五。 凡為八節二十四氣。氣損益九寸九分六分分之一。

不只周髀算經，各曆書中都會記錄節氣的晷影，越到後代越精確。但能在該節氣時測量晷影，表示節氣當有其定義法，是怎麼定義的呢？這定義又是否曾改變過？另外周髀算經這裡的數字顯然有問題，春秋分的晷影絕對不可能是夏冬至晷影長的平均值，這些在之後文章還會細述，但即使真的測量準確。曆法中的節氣不可能是用這個方法推定的，因為總不能測完之後再宣布某節氣是哪一天，還是要能先事先推測才行，測量是用來記錄驗證與修正用的。

在臺灣，清明寒食時節吃春捲 (圖片來源：Wikipedia)

古代推算測量節氣，太初曆以前沒有明確文字記載，僅能從片段的記錄推知，我們在此不討論，而從有明確文字記載的太初曆三統曆開始即是使用「平氣」。雖然「定氣」的概念很早就有，但一直到清初改用時憲曆時才將「定氣」用於曆法，「定氣」的部分其他文章還會提及。

「平氣」是指直接把回歸年等分成$24$等分，再直接從冬至點的那個時刻累加而得。 因為下一篇文章的關係，我們這裡先以唐代時唐肅宗頒布的太衍曆為例， 

 根據【新唐書卷二十八上 志第十八上 曆四上】：
《開元大衍曆》演紀上元閼逢困敦之歲，距開元十二年甲子，積九千六百九十六萬一千七百四十算。

以策實乘積算，曰中積分。盈通法得一，為積日。爻數去之，餘起甲子算外，得天正中氣。凡分為小餘，日為大餘。加三元之策，得次氣。 

看起來很複雜，但其實不會，裡面只是加減乘除而已，常數都有附上，只因為是文言看起來比較複雜：

通法三千四十。

策實百一十一萬三百四十三。 

三元之策十五，餘六百六十四，秒七。

「通法」$3040$，指的是把一天分成幾等分，「策實」$1110343$，指的是一年共有幾個「通法」的等分，把「策實」除以「通法」就是一個回歸年有幾天，也就是$\frac{1110343}{3040}=365.2444$，所以在大衍曆中推算的回歸年是$365.2444$天。

「三元之策」指的是兩個節氣間隔幾天，因為用的是平氣，所以就是回歸年等分成$24$個節氣： $$\begin{align*} \frac{1110343}{3040} \times \frac{1}{24} &= 365 \frac{743}{3040} \times \frac{1}{24} \\ &= 365 \times \frac{1}{24} + \frac{743}{3040} \times \frac{1}{24} \\ &= 15 \frac{5}{24} + \frac{743}{3040} \times \frac{1}{24} \\ &= 15 + \frac{5}{24} + \frac{743}{3040} \times \frac{1}{24} \\ &= 15+ \frac{5 \times 3040 + 743}{3040} \times \frac{1}{24} \\ &= 15 + \frac{15943}{3040} \times \frac{1}{24} \\ &= 15 + \frac{664 \times 24 + 7}{3040} \times \frac{1}{24} = 15 \frac{664+\frac{7}{24}}{3040} \end{align*}$$

所以三元之策是$15 \frac{664+\frac{7}{24}}{3040}=15.21852$，也就是上文中出現的「三元之策十五，餘六百六十四，秒七。」秒七的分母未明寫，但這裡的秒也不是現今相同的單位，只是更小的次單位，但推算的來源應如上述所示，方便起見我們之後直接用回歸年除以$24$計算上或視覺上可能更簡單些。

「積算」就是上元積年，如果算到開元十二年(西元$724$年)的剛過的那個冬至則如上述所寫共有$96961740$年(上一篇有提及，曆書中描述上元積年都是描述到所指年的剛過的那個冬至以方便計算)。以「策實」乘「積算」盈「通法」，其實就是$96961740 \times 1110343 \div 3040$，即從上元算到開元十二年剛過的冬至共有幾天，也就是$96961740$年乘以一個回歸年有幾天。

「分為小餘，日為大餘」把上述的天數除以$60$得到的餘數，整數部分(就是大餘)可以知道是哪一天，分數的部分(就是小餘)可以知道冬至點的時刻。

「加三元之策，得次氣。」若要計算開元十二年的夏至，因為冬至到夏至過了12個節氣，從冬至點再加$365.2422 \times \frac{12}{24}$天，也就是夏至的時刻。而除以$60$得到的餘數，「大餘」可以算出是哪一天，「小餘」可以知道是哪一刻。算式如下：

先計算到上元到開元十二年剛過的那個冬至有幾天：$\frac{1110343 \times 96961740}{3040}$，

再加上冬至到夏至過了$12$個節氣：

$\frac{1110343 \times 96961740}{3040} + \frac{1110343}{3040} \times \frac{1}{24} \times 12 = 35414733497.3656$ ，

所以上元到開元十二年的夏至共有$35414733497.3656$天，把這個數字除以60的餘數中的「大餘」便可知道天干地支記日是何日，從「小餘」可知道是哪一刻：

$35414733497.3656 \equiv 17.3656\ ( mod\ 60)$ ，把小數點化為分母為$3040$的分數，

$0.3656 \times 3040 = 1111$，所以 $17.3656 = 17 \frac{1111}{3040}$，小餘$1111$，大餘$17$。

查表可知大餘$17$所以是辛巳日，但跟上一篇一樣，如果參考萬年月曆的網站軟體程式等，因其都是用這個方法推算的，因此算出來一樣是必然的結果，當然這其實跟實際上的日月運行不同畢竟當時觀測與天文觀還是有限制。

---

上一篇推算冬至，筆者暫時沒能找到驗證的文章，不過節氣共有二十四個，提到其他節氣的文章就比較多了，筆者搜尋維基文庫查到了這篇元稹的祭文：

元稹【秋分日祭百神文】 維長慶元年歲次辛丑八月甲子朔十八日辛巳，皇帝遣通議大夫行內侍省常侍賜紫金魚袋李某，祭於百神之靈：朕奄宅萬有，亭毒品類，日月所照，永思和寧，上極於天，下蟠於地，包山絕海，窮冥入元，至於毛鱗躶羽之神，鹹秩無文，以祛不若。秋序始肅，時將順成，且報且祈，用舉常祀。罔害嘉穀，以貽神羞。

標題都寫秋分日了，應該是那天寫的吧。文章的第一句直接寫出是農曆的哪一年哪一月哪一天，那就讓我們來算算長慶元年 (西元$821$年) 的秋分日究竟是不是辛巳日吧！ 

首先要先知道當年所用的曆法及其常數，簡單google查詢可以知道長慶元年使用的是「觀象曆」(西元$807$年 - 西元$821$年)。「觀象曆」在新唐書中有記錄：

【新唐書卷三十上 志第二十上 曆六上】 憲宗即位，司天徐昴上新曆，名曰《觀象》。起元和二年用之，然無蔀章之數。至於察斂啟閉之候，循用舊法，測驗不合。

寫得不甚清楚，我們剛好就是需要蔀章之數。只好查閱舊唐書：

【舊唐書卷三十二志第十二曆一】 憲宗時，徐昂造《觀象曆》。其法今存，而元紀蔀章之數，或異前經；而察斂啟閉之期，何殊舊法。

還是沒寫清楚，而且「或異前經」，這下有點麻煩。不過難得有古文能幫助驗證，讓我們姑且使用前一個曆「建中正元曆」來計算，如果天數有差最多差到一兩天，雖然不是很好的驗證方式，不過畢竟是大文學家元稹寫的，使用名家的作品算起來比較有感覺，後段還會有其他文章可供驗證。

【新唐書卷二十九 志第十九 曆五】 《建中正元曆》演紀上元甲子，距建中五年甲子，歲積四十萬二千九百算外。 　　 《正元》通法千九十五。策實三十九萬九千九百四十三。 三元之策十五，餘二百三十九，秒七。

可以看到上元到建中五年 (西元$784$年) 共有$402900$年。建中是唐德宗的年號，因為建中五年那一年改曆且改年號為興元，建中五年(西元$784$年)就是興元元年甲子年。元稹寫的祭文是在長慶元年(西元$821$年)，所以從上元到長慶元年共 $402900+37$年。

這裡正元曆的用詞也是「通法」$1095$為一天切成幾等分，「策實」$399943$為一個回歸年有幾個「通法」的等分，所以正元曆的回歸年長度是$\frac{399943}{1095} =365.2447$天。

那計算上元到長慶元年剛過的那個年底冬至就是 $(402900+37) \times \frac{399943}{1095}$天。

「正元曆」的「三元之策」(兩個節氣相距的天數)用的是$15 \frac{239+\frac{7}{24}}{1095}$，同樣也就是回歸年$\frac{399943}{1095}$除以$24$照之前推算方法來的，用後者回歸年除以$24$更簡單些。

元稹寫的時間點是秋分日，是冬至後第$18$個節氣， 所以從上元到長慶元年的秋分共有$(402900+37) \times \frac{399943}{1095} + \frac{399943}{1095}\times \frac{18}{24} = 147170897.3043$ 天，而除以$60$的餘數則為$17.3043$，小數點要用分母為$1095$的分數表示，也就是$0.3043 \times 1095 = 333$左右。

所以除以$60$的餘數是$17 \frac{333}{1095}$，大餘是$17$，小餘是$333$。小餘是表示秋分點的時刻其實這裡我們用不到，但大餘可以知道是哪一天，我們查表可知$17$即為辛巳！跟元稹寫的一樣！

可惜這是用前一個曆法計算的，不是真的很好的驗證方式，我們再換個例子好了，筆者繼續從維基文庫中找到了這篇文章，不過這就是單純史書中的記事而不是大家熟知的文學家寫的文章了：

【南齊書卷九志第一禮上】 又尋景平元年正月三日辛丑南郊，其月十一日立春，元嘉十六年正月六日辛未南郊，其月八日立春，此復是近世明例，不以先郊後春為嫌。

景平 (西元$423$年 - 西元$424$年) 是南朝劉宋宋少帝的年號，元嘉 (西元$424$年 - 西元$453$年) 是南朝劉宋宋文帝的年號，景平二年時宋少帝過世，年號即換成元嘉元年。景平元年 (西元$423$年) 與元嘉十六年 (西元$439$年) 皆使用「景初曆」，「景初曆」在宋書中有記錄：

【宋書卷十二志第二】 壬辰元以來，至景初元年丁巳，歲積四千四十六，算上。此元以天正建子黃鍾之月為曆初，元首之歲夜半甲子朔旦冬至。 紀法，千八百四十三。 周天，六十七萬三千一百五十。 推二十四氣術曰：置所入紀年，外所求，以餘數乘之，滿紀法為大餘，不盡為小餘。大餘滿六十去之，餘命以紀，算外，天正十一月冬至日也。 求次氣，加大餘十五，小餘四百二，小分十一，小分滿氣法從小餘，小餘滿紀法從大餘，命如前，次氣日也。

「壬辰元」表示這裡用的上元不是習慣用的「甲子年」而是「壬辰年」。可以看到上元到景初元年 (西元$237$年) 共有$4046$年，不過景初元年 (青龍五年) 是個曆法上有點複雜的一年，那年魏明帝改正朔以建丑為歲首還砍掉三月份。可能是因為有點複雜的關係，這裡描述的上元積年是真的算到景初元年年底的那個冬至，與其他曆書的習慣算到前一年年底的冬至不太一樣，所以計算的時候要少算一年，如果照其他曆習慣的寫法會是壬辰元到景初二年戊午年 (西元$238$年) 共有$4046$年，我們用後者來計算比較不會混淆。

景初二年 (西元$238$年) 跟我們要算的景平元年 (西元$423$年) 相距$185$年。

這裡景初曆的用詞是「紀法」$1843$為一天切成幾等分，「周天」$673150$為一個回歸年有幾個「紀法」的等分，所以景初曆的回歸年長度是$\frac{673150}{1843} =365.2469$天。

那計算上元到景平元年 (西元$423$年) 剛過的那個年底冬至就是 $(4046+185) \times \frac{673150}{1843}$天。

「景初曆」的兩個節氣相距的天數如上述用的是$15 \frac{402+\frac{11}{12}}{1843}$，同樣也就是回歸年$\frac{673150}{1843}$除以$24$照之前推算方法來的，用後者回歸年除以$24$更簡單些。

文中寫的時間點是立春日，是冬至後第$3$個節氣， 所以從上元到景平元年的立春共有$(4046+185) \times \frac{673150}{1843} + \frac{673150}{1843}\times \frac{3}{24} = 1545405.20550733$ 天，而除以$60$的餘數則為$45.20550733$，小數要用分母為$1843$的分數表示，也就是$0.20551 \times 1843 = 378$左右。

所以除以$60$的餘數是$45 \frac{378}{1843}$，大餘是$45$，我們查表可知$45$即為己酉，對照原文「三日辛丑，其月十一日立春」，辛丑日後八日，沒錯也真的是己酉！文中另一個元嘉十六年的立春也可以用同樣的方式計算，讀者可以自行驗證！如同上篇所述，如果查閱萬年曆網站程式資料，也都是從這些史書的數據中推出的，不便拿來當驗證的工具，唯有直接對照當時的文章留下的記錄才適合。

希望這篇能讓大家對於當時如何推算有更進一步的了解！

二十四節氣 (4) ：如何推算冬至是未來的哪一天？

在農曆中，決定一個回歸年 (以現在的觀點就是地球繞太陽公轉的日數) ，是從「冬至」起算到下一個「冬至」。決定哪個月是正月要靠節氣，也就是太陽地球的相對位置，即太陽的運行 (當時的天文觀) ，其中最重要的節氣即為冬至。因此，冬至是訂立農曆最重要的一天。

但是這天是怎麼定的呢？用說的很簡單，立竿測影，在正午時分所測的竿影，最長的那一天即為冬至。可是月曆不能這樣定，月曆是要預先頒布的，總不能天天測，測了確定哪天竿影最長再定那天為冬至，這樣的月曆永遠會落後現實生活。另外，測了多年之後還會發現，冬至似乎有個精確的時刻，因為若用同樣的方法測竿影，每年那個最長的竿影，可能不一樣長。不會長於某個值，也不會短於某個值，似乎要剛好在某個時間點才會最長，卻不一定在正午，可是那個時刻如果不在正午又觀測不到。長久下來，推估那個時間點便會是建立曆法很重要的一步。

冬至一定要吃湯圓的啊 (圖片來源：Wikipedia)

曆法是要能預測日月星辰的，也就是要用已知的數據來推算未來。實際觀測的結果能用來校正推測的結果，但總還是要有個推算的方法才行。這篇文章要介紹的是，當規則確立之後，是怎麼透過定好的數值來推算。至於如何求得拿來推算的觀測數據，如著名的祖沖之定冬至法則會在日後繼續說明。

古代曆法的推算是利用「上元積年」的方式，來外插推測各節氣與日月星辰的運行。關於上元積年的細述會有專文解說，在此先簡單說明：上元是個想像中的日子，即各個重要天文曆法現象同時發生的那一天那一刻，甲子年甲子日午夜零時冬至且朔時，加上金木水火土星交會於冬至點等，把這個再巧不過的日子當成原點，只要各個天文曆法節氣的日子都是遵照一定的規律，那就可以用外插的方式推斷出哪一個時節是哪一天哪一刻。

概念其實很簡單，例如假設一個回歸年是 $365.2422$ 天 (因為地球軌道的關係這其實是平均數字，而且回歸年的長度因為歲差等的關係也慢慢在改變但每年變動很小，之後會再提及)，又假設今年的冬至點剛好是在凌晨$0$時$0$分，且那一天也是甲子日，一年後的冬至點與冬至日是在什麼時候呢？

答案不難，當然就是$365.2422$天之後。那若是要快速算出該日以天干地支記日是哪一天，要怎麼算呢？也不難，把 $365.2422$ 除以 $60$ 得到的餘數便是，也就是 $5.2422$，所以一年後的冬至日會是甲子日後過$5$天，也就是己巳日，而確切的時間點便是 $0.2422$ 日，換算成現在的時刻表示法則會是 $0.2422 \times 24 = 5.8128$， $0.8128 \times 60 = 48.768$，$0.768 \times 60 = 46.08$，也就是早上$5$時$48$分$46.08$秒。所以我們只要知道那個想像中的日期是什麼時候，再知道與我們想算的日子相距多久，又知道一個回歸年有多長的話，我們便可以算出冬至的時刻。

這些資料都可以從我們熟知的史書如二十四史中得到，讀者們可能曾經讀過二十四史裡的文章，譬如最常見的史記、漢書中描寫人物的部分，像是秦始皇本紀、項羽本紀等，不過這些史書中同時也有「志」，如「禮樂志」、「刑法志」等，曆法會歸在「志」這部分，所以這些正史中都有明確記載當時曆法的使用數據。

這些數字是從天文觀測以及推算出來的，我們在此不細談這些數字的來源，畢竟當年的觀測沒有現代準確，天文觀也不是當代的天文觀，所以用現代的眼光來看當然是錯誤百出，怎麼觀測與推導出這些錯誤的數字我們就先不深究，但這些數字就是當時使用的曆法，所以這些數字對於我們了解曆法的制定是有幫助的。

我們就從最早有明確文字記載的太初曆 (西元前$104$年 - 西元$4$年) 來看起吧，但史記或漢書中並沒有詳細列出其使用數據，而從太初曆稍加修改來的三統曆 (西元$5$年 - 西元$84$年) 開始，史書大多記載得很清楚。因為三統曆算是沿用其數據，所以從三統曆的記錄可以看到當時太初曆的一些記錄。其實之後一直到大元時開始使用的授時曆 (西元$1281$年-西元$1387$年) 之前都是利用上元積年的方式來推算冬至，直到授時曆時才改掉。這之中還慢慢有引進歲差，這些部分之後還會提及。

太初曆當初改曆的其中一個小原因是因為認為太初元年 (西元前$104$年) 又到了甲子朔旦冬至，也就是太初元年時剛過的那個冬至(前一年年底)，冬至點的時刻剛好又是夜半，夜半時也剛好是朔時，又正好是甲子日。以現在的說法來說：這是一個 sign...

來看看最早有記錄數據的三統曆怎麼寫的：

【漢書卷二十一律曆志第一】漢曆太初元年，距上元十四萬三千一百二十七歲。前十一月甲子朔旦冬至。

太初曆與三統曆所算出使用的上元，如上述所示為 太初元年 (西元前$104$年) 的 $143127$ 年前，這裡的「上元積年」算到的是太初元年剛過的前一年年底的那個冬至。讓我們來實地算算看吧！不過筆者翻閱了史料，暫時沒發現有什麼直接可供驗算的文獻，如果查閱一些編輯萬年農曆的程式網站軟體之類的，他們的建構來源也都是從史書中這些史料來的，所以與他們相符是必然的結果。我們就直接算算太初元年前一年的那個冬至是不是真的是甲子日且冬至點正巧在夜半時好了。

【漢書卷二十一律曆志第一】推冬至，以算餘乘人統歲數，盈統法得一，名曰大餘，不盈者名曰小餘。除數如法，則所求冬至日也。 

這裡雖然是寫「算餘」乘「人統歲數」，不過這兩個數是從其他數再運算而來的，又因為這是「三統曆」，有天統、地統、人統，所以用詞刻意用得有點玄，但我們只關心數學的部分，簡單一點我們可以直接從三統曆中的「統法」和「周天」與「上元積年」來算(這些名詞的使用在不同曆書中稍有出入，可能是不同年代不同習慣)，這類型的算法在日後的曆法中有使用到上元積年的也同樣適用。

【漢書卷二十一律曆志第一】
統法千五百三十九。
周天五十六萬二千一百二十。

「統法」是把一天切成幾等分，這類型的切割法只用於曆算，不會在日常生活中出現，畢竟一天切成這個特殊數字等分使用上當然不甚方便，而且古代計時工具也不發達，日常生活中如此細切意義不大。在三統曆中把一天切成$1539$個單位，「周天」則是一個回歸年共有幾個上述的單位，三統曆使用的數字是$562120$個單位。$\frac{562120}{1539} = 365\frac{385}{1539}= 365.2502$，也就是一個回歸年有$365.2502$天。現在看當然知道這不準，不過這已經是兩千多年前的測量與運算了。

那怎麼算從上元到太初元年前一個冬至總共過了幾天呢？也不難，就如同之前提的，一個回歸年幾天乘以經過多少個回歸年即可，太初曆或三統曆使用的上元積年如上述所示到太初元年 (西元前$104$年) 是$143127$年，所以算式如下：

$$\frac{562120}{1539} \times 143127 = \frac{562120 \times 143127}{1539} = \frac{80454549240}{1539} = 52277160$$

也就是從上元到太初元年的前一個冬至正好是$52277160$天，這是一個整數，而且是$60$的倍數，也就是：$52277160 \equiv 0\ ( mod\ 60)$

因為是$60$的倍數，所以我們知道這個日子正好是甲子日，而且因為除以$60$的餘數為$0$連小數點也沒有，所以剛剛好冬至點的時刻即為午夜零時零分。

這當然是刻意湊出來的結果，因為如上述曾說過，當時改曆的其中一個小原因就是因為認為太初元年 (西元前$104$年) 又到了甲子朔旦冬至，所以使用的數字必然要推出這樣的結果。現代的科技觀測進步回推回去我們可以知道這個觀測推論是有誤的，太初元年剛過的那個「冬至」午夜$0$時$0$分並不是真正的冬至點也不是朔時，但是這是當時使用的數據所以也沒什麼能爭論的，畢竟都是兩千年前了，觀測有誤也不是什麼令人意外的事。

我們再回到曆法中描述推算冬至的那個句子：

【漢書卷二十一律曆志第一】推冬至，以算餘乘人統歲數，盈統法得一，名曰大餘，不盈者名曰小餘。除數如法，則所求冬至日也。 

後半段提到了「大餘」與「小餘」。上面的運算因為剛好是$60$的倍數整所以不適合當例子，假設算到太初元年年底的那個冬至就會有這兩個數字了。

讓我們來運算一下。因為多過了一年，所以 $143127+1 = 143128$：

$$\frac{562120}{1539} \times 143128 = \frac{562120 \times 143128}{1539} = \frac{80455111360}{1539} \\ \frac{80455111360}{1539} \equiv 5.250162\ ( mod\ 60)$$

不過當時不會用小數點來表示，會把小數點後的那部分用分數來表示，分母即為之前用的$1539$，所以把$0.250162 \times 1539 = 385$，即餘數為$5 \frac{385}{1539}$。其中$5$即為「大餘」，$385$即為「小餘」。從「大餘」可以推算出天干地支日，「小餘」可以算出冬至點準確的時刻。

當時應該也不會用上述小數的方式計算，我們這裡使用小數的方式只是方便求解而已。其實因為前一年的冬至$0$時已知是冬至點了，簡單一點的算法直接拿$\frac{562120}{1539}=365 \frac{385}{1539}$除以$60$的餘數也是一樣的。

值得注意的是，如果查閱萬年農曆的程式網站軟體等工具，可能會發現太初元年前一年(即元封六年)年底的冬至並不是甲子日，那是因為當時改曆是從太初元年開始改的，所以前一年使用的曆法還是上一部顓頊曆推算的結果，有所出入很正常，而正是因為這些出入才會導致歷史上一直不斷地改曆。

後來的曆法慢慢有將歲差考慮進去，這部分我們在日後還會繼續說明。